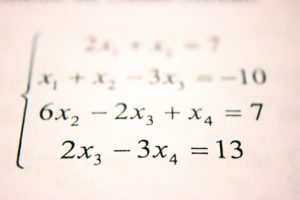
गणिताला आपल्याकडे रूक्ष म्हणण्याची परंपरा आहे. कुणास ठाऊक, केवळ आपल्याकडेच नाही, तर कदाचित ही परंपरा जगभरही असेल. ह्या नितांतसुंदर विषयाला रूक्ष का म्हणायचं ह्याचं उत्तर मात्र कुणाजवळही नसतं. एक फॅशन ह्या पलिकडे ह्याला काही अर्थ नाही हेच खरं.
अर्थात कारणं काही असली तरी ही परंपरा आपल्याकडे तशी शेकडो वर्षं असावी, आणि बहुधा म्हणूनच, गणिताविषयी प्रचंड आस्था असलेल्या आणि ह्या विषयाची उपयुक्तता पूर्णत: ज्ञात असलेल्या आमच्या काही पूर्वजांनी जणू काही ह्या ना त्या प्रकारे ही परंपरा मोडून काढण्याचे प्रयत्न केले. ह्यात प्रामुख्याने येतात भास्कराचार्य! त्यांचा लीलावती ग्रंथ वाचताना ठायी ठायी ह्याचा प्रत्यय येतो. त्यात त्यांनी गणित नुसतं विशद केलं असं नाही तर मोठ्या सुंदर भाषेत त्यांनी ते सर्व मांडलं आहे. लेखनाचे आणि मुद्रणाचे तंत्र विकसित झाले नसल्यामुळे पूर्वीच्या काळी ग्रंथ मुखोद्गतच करावे लागत. आणि मुखोद्गत होण्यासाठी गद्यापेक्षा पद्य अर्थातच सोपे! त्यामुळे बहुतांश प्राचीन ग्रंथ काव्यात्मक भाषेतच लिहिले जात. बहुसंख्य हिंदूंना पूज्य असलेले रामायण, महाभारत हे ग्रंथ घ्या, जगभर कुतुहलाचा विषय असलेली भगवद्गीता घ्या, अलिकडच्या काळात बराचसा विवाद्य ठरलेला मनुस्मृती घ्या, सगळे पद्यमयच तर आहेत की!
इथे लक्षात घ्यायची गोष्ट ही की अभ्यासाचे विषयही त्याकाळी प्रामुख्याने काव्यातच ग्रथिले गेले होते. गणित-विज्ञान-राज्यशास्त्र ह्या सारखे कठीण विषयही जेव्हा काव्याच्या कोंदणात बसवले जात असतील तेव्हा त्यातील ज्ञानाबरोबरच त्यातील काव्याच्या ओढीने तत्कालीन विद्यार्थिवर्ग त्या त्या ग्रंथांच्या परिशीलनास अधिकाधिक उद्युक्त होत असावा. भास्कराचार्यांची श्रेष्ठता ही की त्यांचं काव्य केवळ छंदोबद्ध आहे असं नाही तर त्यात काव्यातील इतर अलंकारही दृष्टीस पडतात. तसंच गणितातील सूत्र समजावल्यानंतर त्यावर जी गणितं आचार्यांनी विचारली आहेत ती वाचतानाही मोठं कौतुक वाटतं. तत्कालीन गुरुकुलपद्धतीत सर्वसामान्यत: गावाबाहेर असलेल्या गुरुगृही जाऊन शिक्षण घ्यावे लागायचे. समाजापासून काहीशा लांब असलेल्या त्या त्या गुरुकुलाभोवती अतिशय रमणीय असा निसर्ग दृष्टीस पडत असे. भास्कराचार्यांच्या लेखनात तो सर्व रम्य परिसर सहज डोकावून जाताना दिसतो. पुढे कधीतरी आपण भास्कराचार्यांच्या लेखनाचा सविस्तर अभ्यास करू तेव्हा ह्यावर सविस्तर भाष्यही करू आणि आचार्यांच्या लेखनशैलीचा अधिक आस्वादही घेऊ.
आर्यभटाबद्दल असं सांगता येईल की त्याने संख्यालेखनासाठी एका वेगळ्याच संकल्पनेचा आधार घेतला होता. ही कल्पना किंवा पद्धत सर्वप्रथम त्यानेच निर्मिली होती का ते सांगता येत नाही, मात्र त्याच्या आर्यभटीय ग्रंथामुळे ती लोकप्रिय होण्यास मदत झाली असावी. ह्यात विविध संख्यांसाठी विविध अक्षरे योजून त्यातून संख्यांसाठी वेगवेगळे शब्द त्याने तयार केले होते. गेल्या लेखात आपल्या पूर्वजांनी विविध संख्यांसाठी योजलेले व वापरलेले शब्द आपण पाहिले. त्यात आणि आर्यभटाच्या पद्धतीत फरक काय असा प्रश्न पडू शकतो. मूलभूत फरक असा की ते सर्व योजलेले शब्द मुळात अस्तित्वात होतेच. ती ती वस्तू त्या त्या मात्रेत किंवा प्रमाणात उपलब्ध असल्यामुळे त्या त्या संख्येला ते ते शब्द योजले गेले होते (उदा. १ साठी इन्दू, २ साठी कर वगैरे). मात्र आर्यभटाचं वैशिष्ट्य हे की त्याने योजलेल्या संख्या-अक्षर पद्धतीतून नवनवीन शब्द तयार झाले व हे त्याने वापरले. ह्या नव्या शब्दांना तसा एरवी अर्थ काहीच नव्हता. केवळ त्या विशिष्ट संदर्भातच ते अर्थवाही ठरत होते. मात्र त्यांचं रूप मोठं गमतीशीर होतं. आर्यभटीयाच्या दुसऱ्याच काव्यपंक्तीत आर्यभट म्हणतो,
वर्गाक्षराणि वर्गेऽवर्गेऽवर्गाक्षराणि कात् ङ्मौ य:।
खद्विनवके स्वरा नव वर्गेऽवर्गे नवान्त्यवर्गे वा॥
ह्याचा सर्वसामान्य अर्थ असा की त्याने ‘क्’ पासून ‘म्’ पर्यंत अक्षरांना १ ते २५ अशा संख्या बहाल केल्या. म्हणजे त्याच्या ग्रंथात संख्यावाचक शब्दात जिथे जिथे ‘क्’ येईल, तिथे १ ही संख्या धरायची. ह्याच न्यायाने ख् म्हणजे २, ग् म्हणजे ३, असं करत करत म् म्हणजे २५! त्याच बरोबर अ ते औ स्वरांना त्याने १, १०, १००, वगैरे दहाच्या पटीतील संख्या ठरवल्या. ह्यातून ख्युघृ, ढुङि, ख्रिच्युभ वगैरे अनेक गमतीशीर शब्द तयार झाले आणि आर्यभटीयात आपापल्या जागी स्थानापन्न झाले. प्रस्तुत ग्रंथात त्याने त्रिकोणमितीवर फार महत्त्वपूर्ण भाष्य केले आहे. मात्र त्याच्या ह्या संख्या-अक्षर पद्धतीमुळे त्याची रचना कशी होते ते त्रिकोणमिती संदर्भातील एका उदाहरणावरून समजेल…
मखि भखि फखि धखि नखि ञखि ङखि हस्झ स्ककि किष्ग श्घकि किध्व
घ्लकि किग्र हक्य धकि किच स्ग झश ङ्व क्ल प्त फ छ कलार्धज्या:॥
एकएकट्याने वाचतानाही चेहऱ्यावर किंचित स्मितहास्य पसरवणाऱ्या ह्या आर्यभटाच्या काव्यपंक्ती त्यांच्या ह्या विलक्षण शब्दरचनेतून स्मरणात ठेवायला खरंतर सोप्याच जात असल्या पाहिजेत ह्यात शंका नाही.
ह्याचबरोबर गणिताला मनोरंजक करण्यातला आणखी एक प्रयत्न म्हणजे ‘जादूचा चौरस’ सारख्या गोष्टींचा विचार! नारायण पंडिताच्या ‘गणित कौमुदी’ ह्या ग्रंथात हा एक आगळावेगळा प्रकार बघावयास मिळतो. अलिकडच्या काळात ‘सुडोकू’ हा कूटप्रकार सर्वसामान्यांमध्ये बराच लोकप्रिय झाला आहे. ह्या सुडोकूच्या काहीसा जवळ जाणारा, तरीही वेगळा (आणि कदाचित जास्त अवघड) असा हा जादूचा चौरस होता. हा नेमका काय प्रकार होता हे गणित कौमुदीतीलच एका उदाहरणावरून लक्षात येईल.
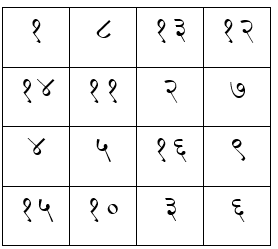
ह्यात प्रत्येक ओळीतील आकड्यांची बेरीज करून पाहा, ती येते ३४. आता प्रत्येक स्तंभातील आकड्यांची बेरीज करून पाहा; तीही येते ३४! इतकंच कशाला, आता त्या चौरसाच्या दोन कर्णांवर असलेल्या आकड्यांची बेरीज करून पाहा, तीसुद्धा चौतीसच आहे. तसंच त्या मोठ्या बाह्यचौरसात चार लहान चौरस सामावलेले आहेत. त्या त्या चौरसातील आकड्यांची बेरीजही ३४च आहे. आणि हो! एक ते सोळा ह्या आकड्यांनी भरलेल्या सोळा छोट्या चौरसांत एकाही आकड्याची पुनरावृत्ती झालेली नाही.
गणित कौमुदीत असे वेगवेगळ्या बेरजेचे, वेगवेगळ्या आकारांचे चौरस बनवण्याच्या अनेक कृती दिलेल्या आहेत. एकाच वेळी अनेक ठिकाणी लक्ष पुरवू शकणाऱ्या व्यक्तीस ‘अनेकावधानी’ म्हणतात. असे जादूचे चौरस बनवण्याच्या प्रयत्नांतून माणसाच्या बुद्धीस चांगलाच व्यायाम होत असणार. मनुष्य अनेकावधानी होण्यास ह्यातून मदत होत असली पाहिजे. शिवाय हा सगळा मजेमजेचा प्रकार! आजकाल ज्याला ‘रिक्रिएशनल मॅथेमॅटिक्स’ म्हणतात, त्यात मोडणारा. नित्याच्या अभ्यासातून बौद्धिक व्यायाम होतोच, पण ह्या प्रकारांतून मनोरंजनही होते. व्यायामशाळेत जाऊन मार्गदर्शकाच्या निरखणाखाली केलेला व्यायाम आणि आजूबाजूचे चार समवयस्क जमवून खेळलेले मैदानी खेळ ह्यात जो फरक आहे तोच इथेही आहे. जाता जाता ह्याच कौमुदीतील एक सुरेख आकृती पाहूया.
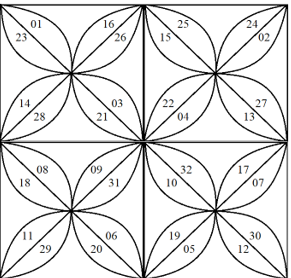
ह्या आकृतीला नारायण पंडित ‘पद्म’ असे नाव देतो. ह्याची गणिती गंमत पाहा. ह्यात १ ते ३२ आकडे घेतले आहेत. प्रत्येक आकडा एकेकदाच वापरला गेला आहे. प्रत्येक लहान चौरसात असलेल्या आकड्यांची बेरीज करा. ती येते १३२. प्रत्येक ओळीतील संख्यांची बेरीज करून पाहा; तीसुद्धा आहे १३२. (अगदी वरच्या ओळीत २३, ०१, १६, २६, १५, २५, २४, ०२ असे आकडे आहेत. अशा एकूण चार ओळी आहेत). प्रत्येक स्तंभातील आकड्यांची बेरीज करून पाहा. ती येईल १३२. (डावीकडच्या पहिल्या स्तंभात ०१, २३, १४, २८, ०८, १८, ११, २९ असे आकडे आहेत. असे एकूण चार स्तंभ विचारात घेता येतील.) इतकंच कशाला, मूळ चौरसाच्या प्रत्येक कर्णावर असलेल्या आकड्यांची बेरीज करून पाहा. तीसुद्धा १३२च आहे!!
“गणित खरंच रूक्ष आहे का?” ह्या प्रश्नाचे नकारार्थी उत्तर अशा आगळ्यावेगळ्या पद्धतीने आमच्या पूर्वजांनी देऊन ठेवलं आहे. पण आम्ही असे कर्मदरिद्री की ते ग्रंथ उघडून बघायलाही आमच्याकडे वेळ नसतो!!!
या लेखमालेतील तिसरा लेख इथे वाचा .
Views expressed in the article are of the author and does not necessarily reflect the official position of Mimamsa: An Indic Inquiry
Author : सलिल सावरकर
सलिल सावरकर हे श्रीमती सी.एच.एम. महाविद्यालयाच्या गणित विभागात सहायक प्राध्यापक म्हणून कार्यरत आहेत. गणितासह संगीत, संस्कृत, खगोलशास्त्र अश्या अनेक विषयांमध्ये त्यांना गती आहे .

नमस्कार गुरुजी, खूप नविन गोष्टी समजत आहेत या लेखांमधून. अजून असेच लेख वाचायला आवडतील. स्तुत्य उपक्रम आहे हा.